my blog

Coding the Beauty of Lagrange Interpolation

What Is A Lagrange Interpolation?

Interpolation is a mathematical technique or method used to approximate or estimate values between known data points. In the context of mathematics, interpolation involves constructing a function that passes through a series of given data points. By using this interpolation function, we can find precise or approximate values between those data points.

Interpolation has numerous applications in various fields. In physics, interpolation can be used to obtain estimates of values at times or locations that are not directly measured. In computer science and computer graphics, interpolation is used to create smooth visual effects, such as object motion or color transitions between frames. In data analysis, interpolation can help fill in missing or unavailable values in a dataset, allowing for more comprehensive and accurate analysis.

There are various interpolation methods, including polynomial methods like Lagrange or Newton interpolation, spline methods, or other approaches like trigonometric interpolation. Each method has different principles and advantages depending on the data characteristics and the desired objectives.

Lagrange interpolation is one of the commonly used methods. It utilizes the Lagrange polynomial to connect the known data points and obtain an interpolating polynomial that passes through those points. The Lagrange polynomial is constructed by dividing each data point by factors involving the differences between data points.

In general, interpolation is a method or process of constructing a function or equation using several known points or sample points to predict or estimate values at other points whose values are not known. For example, there are several points (x_0, y_0), (x_1, y_1), and so on. From these points, a function or equation will be formed, so that for a different value of x or x_a, the value of y or y_a can be predicted/estimated.

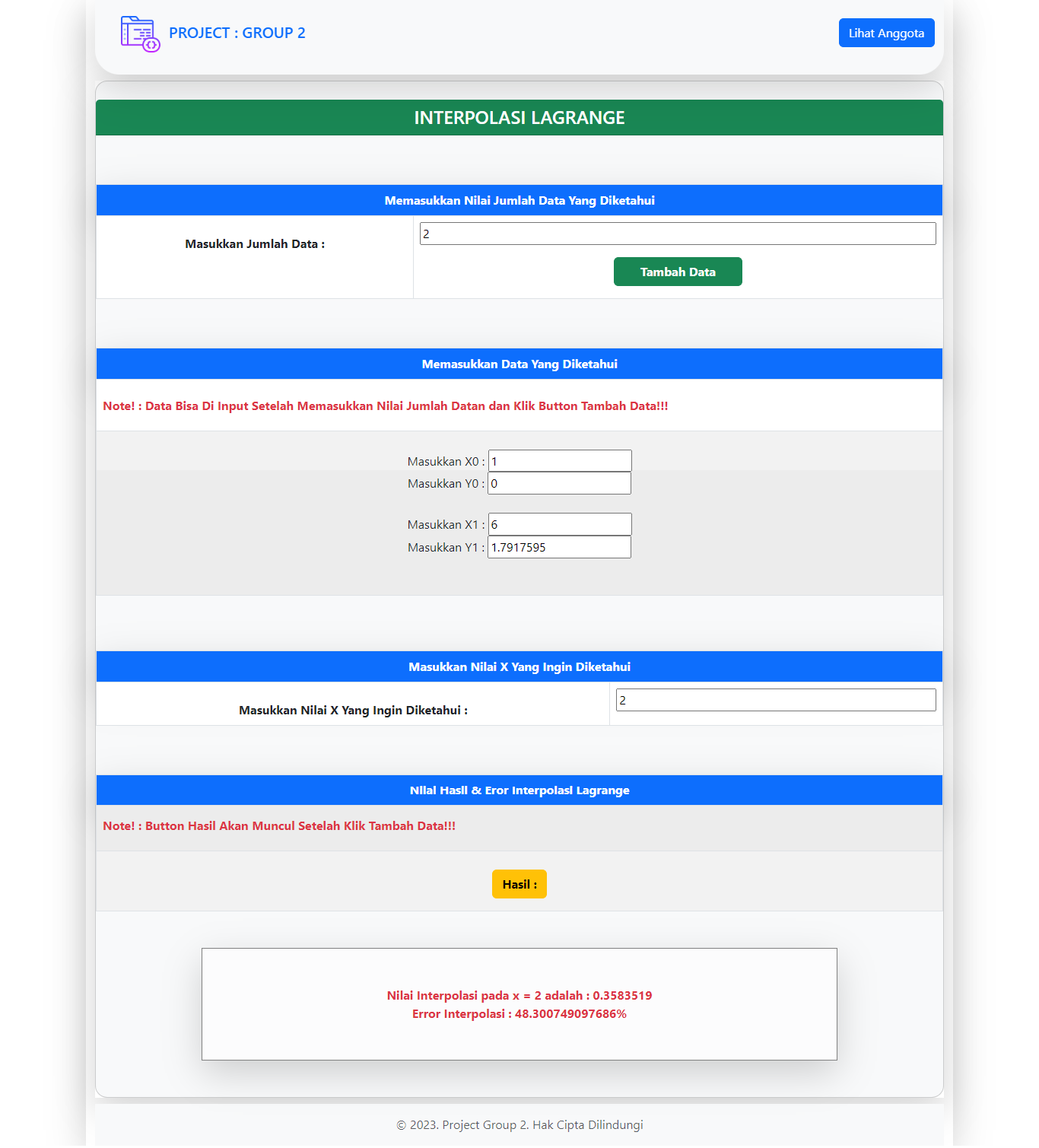
System Overview:

A brief description of the program we created, in the form of inputting data with integer/float data types, where we can input known data/information to find interpolation values more freely (Solving some interpolation tasks only using the program above). When the program is executed, we are required to first input the number of known data, in order to input data for x and y values that are known (also using input), according to the previously inputted data count. For example, if there are 2 known data points for x and y, we must first input the number of known data: 2, then the program will proceed to the next step, which is to input the known data, according to the count, because there is a looping process (for loop) that generally starts from 0 to the number of known data (n); as explained above, we can input the data for data 0: x0 and y0, and data k-1: x1 and y1.

After inputting all the known x and y data, the program processes the next code, which is to print the information of the known x and y data that we have previously inputted, and then instructs us to input the value of x data for which we want to know the interpolation value of y. Once we have inputted that, the program will process the next code to display the interpolated value result, and any errors that may occur.